Citation
“Exposing Fine-Grained Parallelism in Algebraic Multigrid Methods”
Nathan Bell, Steven Dalton, and Luke Olson
SIAM Journal on Scientific Computing (accepted)
Abstract
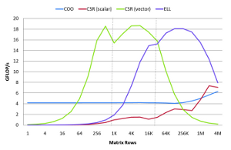
Algebraic multigrid methods for large, sparse linear systems are a necessity in many computational simulations, yet parallel algorithms for such solvers are generally decomposed into coarse-grained tasks suitable for distributed computers with traditional processing cores. However, accelerating multigrid on massively parallel throughput-oriented processors, such as the GPU, demandsalgorithms with abundant fine-grained parallelism. In this paper, we develop a parallel algebraic multigrid method which exposes substantial fine-grained parallelism in both the construction of the multigrid hierarchy as well as the cycling or solve stage. Our algorithms are expressed in terms of scalable parallel primitives that are efficiently implemented on the GPU. The resulting solver achieves an average speedup of 1.8× in the setup phase and 5.7× in the cycling phase when compared to a representative CPU implementation.